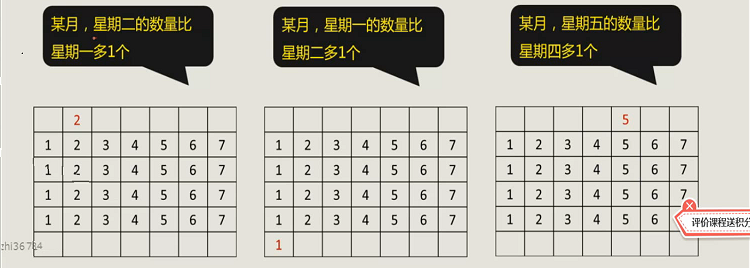
一、必考的行程问题

　　1、行程问题的简单考法

　　

　　

　　

　　

　　

　　

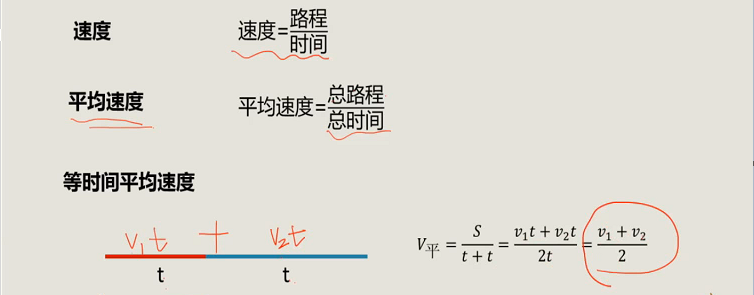
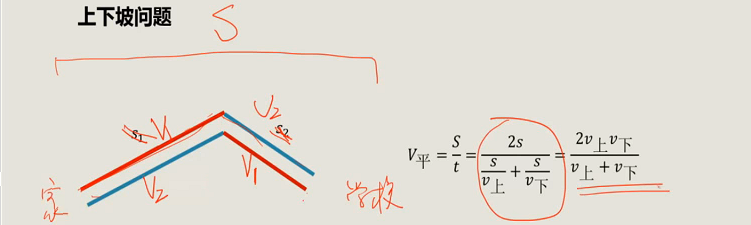
　　【注】上下坡问题其实就是等距离求平均速度的问题。

　　

　　2、相遇问题

• 直线相遇
  
  
  
  
• 环线相遇
  
• 两岸相遇
  【注】单岸相遇和两岸相遇其实是多次相遇问题的变形，并且具备一定的形式：单岸相遇是给出相遇时：第一次距离A的距离为S1，第二次相遇距离A的距离为S2，求AB两地的路程S。规律是：3S1 + S2 = 2S。两岸相遇问题是将单岸相遇的S2改为距离B地的长，其实可以看做单岸相遇问题：S2（单岸） + S2（两岸） = S。但一般不推荐死记硬背，要求能够自己推理出来最好。
  
  

　　3、追及问题

　　

　　

　　

　　

　　

　　

　　4、特别考点—过桥问题

 　　

　　

　　

　　

　　

　　

　　

　　

　　5、特别考点—流水行船

　　

　　

　　

　　

　　

　　6、特殊追击—时钟问题

　　

　　

　　

　　

二、必考的工程问题

　　1、基本考法

　　

　　

　　

　　

　　

　　

　　2、特别考法

　　1）中途休息

　　

　　

　　2）抽调

　　

　　3）轮流

　　

　　4）最优合作

　　

　　【解析】这种求最优解的问题，我们需要将把“最合适的工作”安排个一个人做，再来求其他人该做什么。本题中小王制作甲乙配件的效率都比小刘快，所以，我们应该先将小刘的工作固定下来，即固定“最短板”。然后让小王来配合小刘。小刘制作甲乙的效率比为60:24，即2.5:1，所以效率10天工作全部用于甲配件制作，那么小王需要制作60*10个乙配件，需要600÷75=8天。剩余最后两天，小王效率比为2:1，所以剩下的4/3天做乙部件，2/3天做甲部件，所以可以做100件，最终700件。注：一天内不一定只做一种配件。

　　5）变型——水管问题

　　

三、万变不离其宗的容斥原理

 　　

·　　

　　

　　

　　

　　

　　

　　

　　

　　

　　

　　

　　

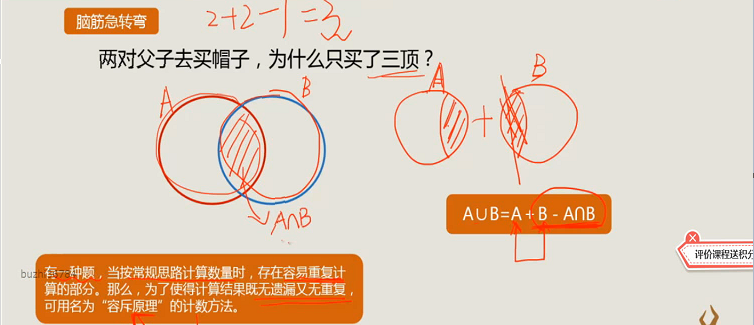
四、千万不能丢分的基本计算题

　　

　　【解析】199219921992=1992（100000000000+10000000+1），同理19911991991也能这样拆分，发现左右两边相等，选C。

　　

　　【解析】画个草图就能模拟出来，选A。

　　

　　

　　

　　

五、命题人偏好的经济利润题

 　　

　　

　　

　　

　　

　　

六、千变万化的几何问题

 　　

　　

　　

　　

　　

　　

七、最不利原理—抽屉原理

　　

　　

　　

　　

　　

　　

　　

　　

　　

八、套路满满的溶液问题

　　

　　

　　

　　

　　

　　

　　

九、吓不倒你的排列组合

　　1、分类法

• 多元问题分类法
  
  
• 定序问题缩倍法
  
• 选排问题先取后排法
  
• 错位排序记公式
  
• 圆桌问题记公式
  

　　2、分步法

• 特殊元素优先法
  
• 捆绑法
  
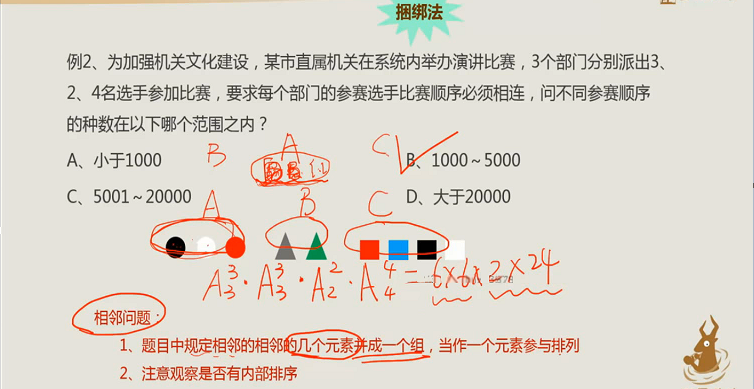
• 插空法
  
• 插板法
  
  
• 反面法
  
  

十、一定几率考的概率问题

 　　

　　

　　

　　

　　

　　

　　

　　

　　

　　

　　

十一、烧脑的统筹问题

　　

　　

　　

　　

　　

　　

　　

十二、简单又常考的年龄问题

　　

　　

　　

　　

　　

　　

　　

　　

十三、常规考法不能丢分的日期问题